- 24 Ara 2023
- 188
- 0
- 16
Konu: Sayı Kümeleri
Kazanım: Sayı kümelerini birbiriyle ilişkilendirir.
Sayıları ifade etmeye yarayan {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarına rakam denir. Doğal sayıları oluşturan rakamlar, birler, onlar, yüzler gibi basamak değerlerine sahiptir. Sayıların basamak değerlerinin toplamı olarak yazılmasına çözümleme denir.
2 nin katı olan tam sayılara çift sayı, 2 nin katı olmayan tam sayılara tek sayı denir.
Tek sayıları T, çift sayıları Ç ile gösterirsek
Ç = {… -4, -2, 0, 2, 4, …)
T = {… -3, -1, 1, 3, …) olur.
Bir çarpımın sonucu tek sayı ise çarpılan bütün sayılar tektir.
Bir çarpımın sonucu çift sayı ise çarpılan sayılardan en az bir tanesi çifttir.
Sayma Sayıları Kümesi (N+ )
N+ = S = {1, 2, 3, ….. }
Doğal Sayılar Kümesi (N)
N = {0, 1, 2, 3, ….. }
Tam Sayılar Kümesi (Z)
Z– = {…, –3, –2, –1} negatif tam sayılar kümesi, Z+ = {1, 2, 3, … } pozitif tam sayılar kümesidir.
Z = Z– ∪ {0 } ∪ Z+ = {…, –3, –2, –1, 0, 1, 2, 3, … }
Rasyonel Sayılar Kümesi (Q)
Q = { a / b : a ∈ Z, b ∈ Z ve b ≠ 0 }
İrrasyonel Sayılar Kümesi (Q′ )
Rasyonel olmayan sayılar kümesidir. kök 2, kök 3 , π , e , … gibi
Reel (Gerçel) Sayılar Kümesi (R)
Rasyonel sayılarla irrasyonel sayıların birleşimine reel (gerçel) sayılar kümesi denir.
R = Q ∪ Q′
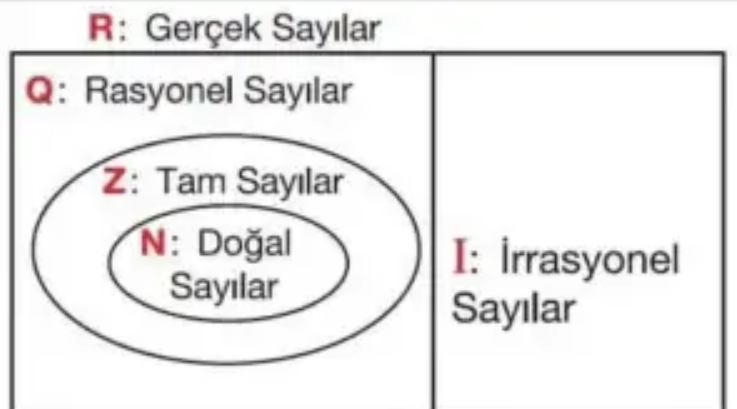
N+ ⊂ N ⊂ Z ⊂ Q ⊂ R
Q′ ⊂ R
Gerçek Sayılar Kümesinde Toplama ve Çarpma işleminin Özellikleri
Toplama İşleminin Özellikleri
1. Kapalılık özelliği: Her a, b ∈ R için a + b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 + 3 = 12 de bir gerçek sayıdır.
2. Değişme özelliği: Her a, b ∈ R için a + b = b + a dır.
9 + 3 = 3 + 9
3. Birleşme özelliği: Her a, b, c ∈ R için a + (b + c) = (a + b) + c dir.
9 + (3 + 5) = (9 + 3) + 5
4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a + 0 = 0 + a = a ise “0” toplama işleminin etkisiz (birim) elemanıdır.
9 + 0 = 0 + 9 = 9
5. Ters Eleman özelliği: Her a ∈ R için a + (-a) =(-a) + a = 0 olduğu için a nın toplama işlemine göre tersi -a dır.
9 + (-9) = (-9) + 9= 0
Çarpma İşleminin Özellikleri
1. Kapalılık özelliği: Her a, b ∈ R için a . b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 . 3 = 27 de bir gerçek sayıdır.
2. Değişme özelliği: Her a, b ∈ R için a . b = b . a dır.
9 . 3 = 3 . 9
3. Birleşme özelliği: Her a, b, c ∈ R için a . (b . c) = (a . b) . c dir.
9 . (3 . 5) = (9 . 3) . 5
4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a . 1 = 1 . a = a ise “1” çarpma işleminin etkisiz (birim) elemanıdır.
9 . 1 = 1 . 9 = 9
5. Ters Eleman Özelliği: Her a ∈ R için ve a ≠ 0 için a . 1/a = 1/a . a = 1 ise a nın çarpma işlemine göre tersi 1/a dır. 0 sayısının çarpma işlemine göre tersi yoktur.
9 . 1/9 = 1/9 . 9 = 1
6. Yutan Eleman özelliği: Her a ∈ R için a . 0 = 0 . a = 0 ise çarpma işleminin yutan elemanı “0” dır.
9 . 0 = 0 . 9 = 0
7. Çarpma işleminin Toplama İşlemi Üzerine Dağılma Özelliği: Her a, b, c ∈ R için
a . (b + c) = a . b + a . c ve
(a + b) . c = a . c + b . c dir.
Bu özelliğe çarpma işleminin toplama işlemi üzerinde soldan ve sağdan dağılma özelliği denir.
Örneğin; 9 . (3 + 5) = 9 . 3 + 9 . 5
9 . 8 = 27 + 45
72 = 72
(9 + 3) . 5 =9 . 5 + 3 . 5
12 . 5 = 45 + 15
60 = 60
Kazanım: Sayı kümelerini birbiriyle ilişkilendirir.
Sayıları ifade etmeye yarayan {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarına rakam denir. Doğal sayıları oluşturan rakamlar, birler, onlar, yüzler gibi basamak değerlerine sahiptir. Sayıların basamak değerlerinin toplamı olarak yazılmasına çözümleme denir.
2 nin katı olan tam sayılara çift sayı, 2 nin katı olmayan tam sayılara tek sayı denir.
Tek sayıları T, çift sayıları Ç ile gösterirsek
Ç = {… -4, -2, 0, 2, 4, …)
T = {… -3, -1, 1, 3, …) olur.
Bir çarpımın sonucu tek sayı ise çarpılan bütün sayılar tektir.
Bir çarpımın sonucu çift sayı ise çarpılan sayılardan en az bir tanesi çifttir.
Sayma Sayıları Kümesi (N+ )
N+ = S = {1, 2, 3, ….. }
Doğal Sayılar Kümesi (N)
N = {0, 1, 2, 3, ….. }
Tam Sayılar Kümesi (Z)
Z– = {…, –3, –2, –1} negatif tam sayılar kümesi, Z+ = {1, 2, 3, … } pozitif tam sayılar kümesidir.
Z = Z– ∪ {0 } ∪ Z+ = {…, –3, –2, –1, 0, 1, 2, 3, … }
Rasyonel Sayılar Kümesi (Q)
Q = { a / b : a ∈ Z, b ∈ Z ve b ≠ 0 }
İrrasyonel Sayılar Kümesi (Q′ )
Rasyonel olmayan sayılar kümesidir. kök 2, kök 3 , π , e , … gibi
Reel (Gerçel) Sayılar Kümesi (R)
Rasyonel sayılarla irrasyonel sayıların birleşimine reel (gerçel) sayılar kümesi denir.
R = Q ∪ Q′
N+ ⊂ N ⊂ Z ⊂ Q ⊂ R
Q′ ⊂ R
Gerçek Sayılar Kümesinde Toplama ve Çarpma işleminin Özellikleri
Toplama İşleminin Özellikleri
1. Kapalılık özelliği: Her a, b ∈ R için a + b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 + 3 = 12 de bir gerçek sayıdır.
2. Değişme özelliği: Her a, b ∈ R için a + b = b + a dır.
9 + 3 = 3 + 9
3. Birleşme özelliği: Her a, b, c ∈ R için a + (b + c) = (a + b) + c dir.
9 + (3 + 5) = (9 + 3) + 5
4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a + 0 = 0 + a = a ise “0” toplama işleminin etkisiz (birim) elemanıdır.
9 + 0 = 0 + 9 = 9
5. Ters Eleman özelliği: Her a ∈ R için a + (-a) =(-a) + a = 0 olduğu için a nın toplama işlemine göre tersi -a dır.
9 + (-9) = (-9) + 9= 0
Çarpma İşleminin Özellikleri
1. Kapalılık özelliği: Her a, b ∈ R için a . b ∈ R dir.
9 ve 3 gerçek sayılardır ve 9 . 3 = 27 de bir gerçek sayıdır.
2. Değişme özelliği: Her a, b ∈ R için a . b = b . a dır.
9 . 3 = 3 . 9
3. Birleşme özelliği: Her a, b, c ∈ R için a . (b . c) = (a . b) . c dir.
9 . (3 . 5) = (9 . 3) . 5
4. Etkisiz (Birim) Eleman Özelliği: Her a ∈ R için a . 1 = 1 . a = a ise “1” çarpma işleminin etkisiz (birim) elemanıdır.
9 . 1 = 1 . 9 = 9
5. Ters Eleman Özelliği: Her a ∈ R için ve a ≠ 0 için a . 1/a = 1/a . a = 1 ise a nın çarpma işlemine göre tersi 1/a dır. 0 sayısının çarpma işlemine göre tersi yoktur.
9 . 1/9 = 1/9 . 9 = 1
6. Yutan Eleman özelliği: Her a ∈ R için a . 0 = 0 . a = 0 ise çarpma işleminin yutan elemanı “0” dır.
9 . 0 = 0 . 9 = 0
7. Çarpma işleminin Toplama İşlemi Üzerine Dağılma Özelliği: Her a, b, c ∈ R için
a . (b + c) = a . b + a . c ve
(a + b) . c = a . c + b . c dir.
Bu özelliğe çarpma işleminin toplama işlemi üzerinde soldan ve sağdan dağılma özelliği denir.
Örneğin; 9 . (3 + 5) = 9 . 3 + 9 . 5
9 . 8 = 27 + 45
72 = 72
(9 + 3) . 5 =9 . 5 + 3 . 5
12 . 5 = 45 + 15
60 = 60


