- 24 Ara 2023
- 188
- 0
- 16
Bu ders notumuzda Matematik Kümeler başlığı altında; Kümelerin Eleman Sayısı, Küme Elamanı, Kümelerin Gösterimi, Küme Çeşitleri, Kümelerde İşlemler, Alt Küme, Özalt Küme, Evrensel Küme, Küme Problemleri, Eşit Küme, Denk Küme, Boş Küme vb. konular hakkında detaylı bilgileri bulabilirsiniz.
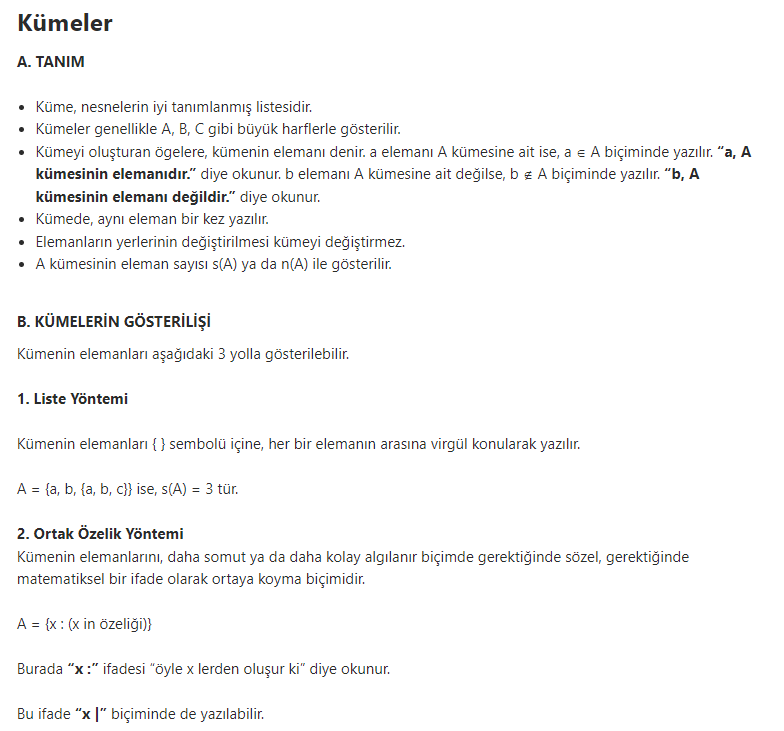
3. Şema Yöntemi
Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak gösterilir.
Bu gösterime Venn Şeması ile gösterim denir.
1. Alt Küme
A kümesi B kümesinin alt kümesi ise A Ì B biçiminde gösterilir.
A kümesi B kümesinin alt kümesi ise B kümesi A kümesini kapsıyor denir. B É A biçiminde gösterilir.
C kümesi D kümesinin alt kümesi değilse C Ë D biçiminde gösterilir.
2. Özalt Küme
Bir kümenin, kendisinden farklı bütün alt kümelerine o kümenin özalt kümeleri denir.
3. Alt Kümenin Özelikleri
Her küme kendisinin alt kümesidir.
i) A Ì A
ii) Boş küme her kümenin alt kümesidir.
Æ Ì A
iii) (A Ì B ve B Ì A) Û A = B dir.
ıv) (A Ì B ve B Ì C) ise, A Ì C dir.
v) n elemanlı bir kümenin alt kümelerinin sayısı 2n ve özalt kümelerinin sayısı 2n – 1 dir.

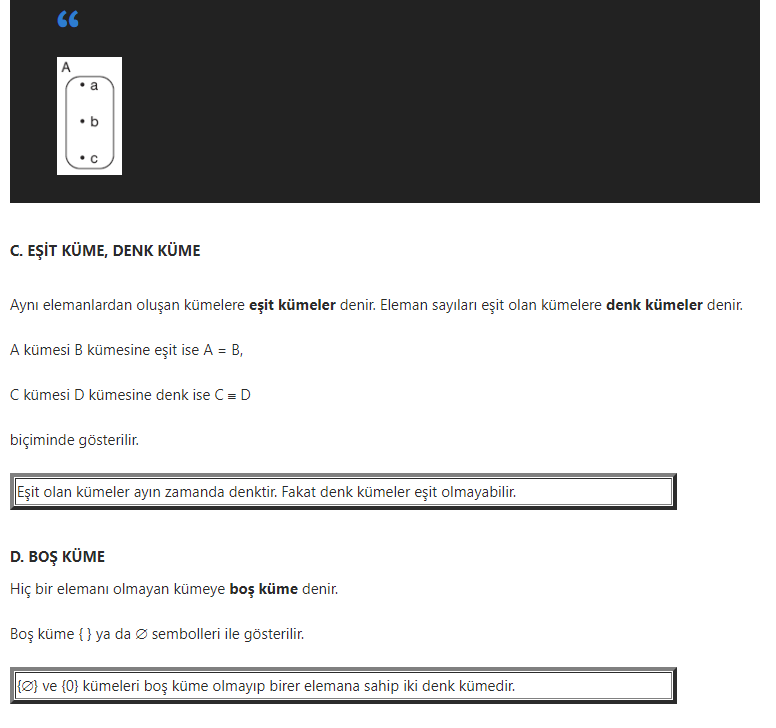
1. Kümelerin Birleşimi
A È B = {x : x Î A veya x Î B} dir.
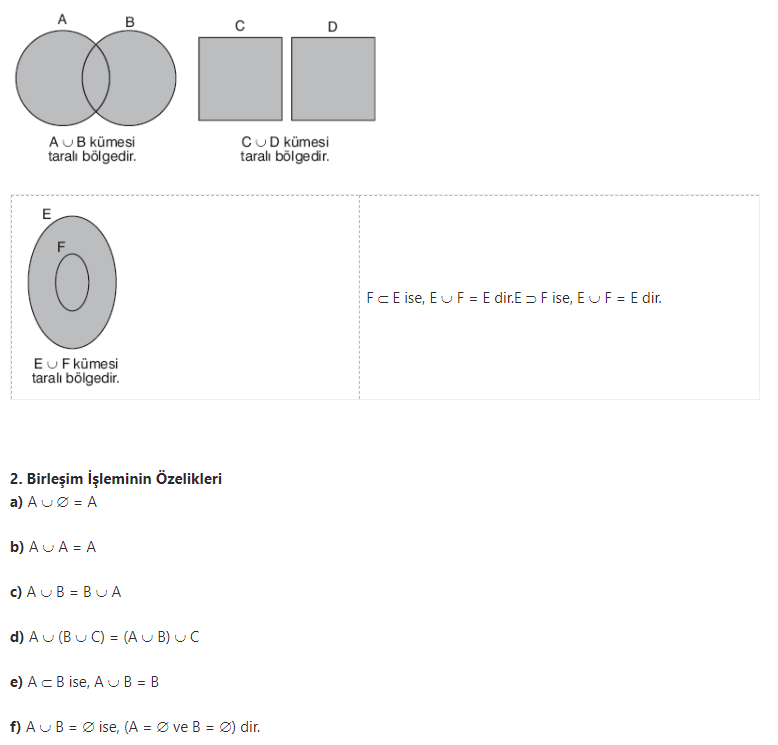
2. Birleşim İşleminin Özelikleri
a) A È Æ = A
b) A È A = A
c) A È B = B È A
d) A È (B È C) = (A È B) È C
e) A Ì B ise, A È B = B
f) A È B = Æ ise, (A = Æ ve B = Æ) dir.
3. Kümelerin Kesişimi
A ve B kümesinin ortak elemanlarından oluşan kümeye A ile B nin kesişim kümesi denir ve A Ç B biçiminde gösterilir.
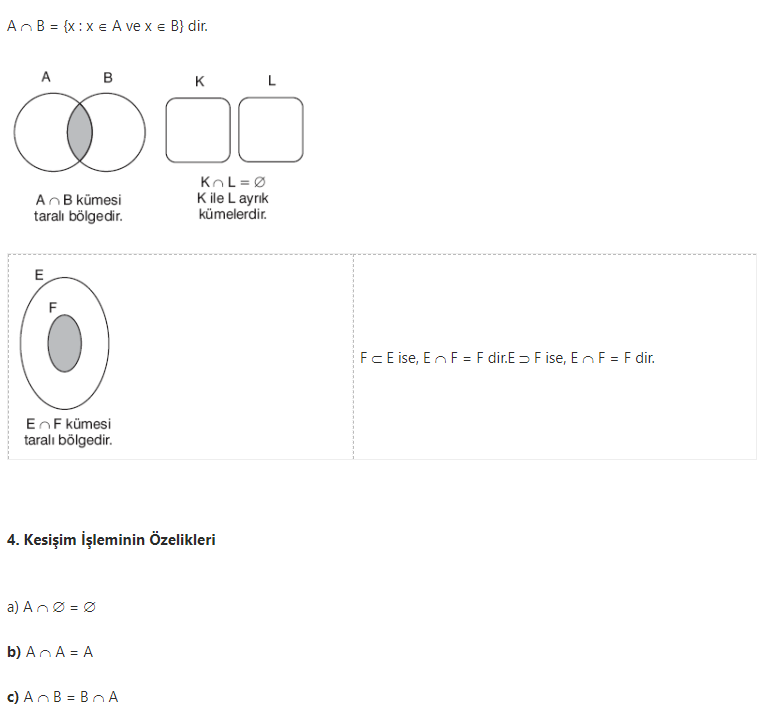
d) (A Ç B) Ç C = A Ç (B Ç C)
e) A Ç (B È C) = (A Ç B) È (A Ç C)
f) A È (B Ç C) = (A È B) Ç (A È C)
I. KUVVET KÜMESİ
Bir kümenin bütün alt kümelerin kümesine kuvvet kümesi denir. Kuvvet kümesi P(A) ile gösterilir.
s(A) = n ise, s(P(A)) = 2n dir.
J. İKİ KÜMENİN FARKI
A kümesinde olup, B kümesinde olmayan elemanların kümesine A fark B kümesi denir. A fark B kümesi A – B ya da A B biçiminde gösterilir.
A – B = {x : x Î A ve x Ï B} dir.


Tenis veya voleybol oynayanların sayısı:
s(T È V) = a + b + c
Tenis ya da voleybol oynayanların sayısı:
s(T – V) + s(V – T) = a + c
Sadece tenis oynayanların sayısı:
s(T – V) = a

Kümeler
3. Şema Yöntemi
Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak gösterilir.
Bu gösterime Venn Şeması ile gösterim denir.
E. ALT KÜME – ÖZALT KÜME
A kümesinin her elemanı, B kümesinin de elemanı ise A ya B nin alt kümesi denir.1. Alt Küme
A kümesi B kümesinin alt kümesi ise A Ì B biçiminde gösterilir.
A kümesi B kümesinin alt kümesi ise B kümesi A kümesini kapsıyor denir. B É A biçiminde gösterilir.
C kümesi D kümesinin alt kümesi değilse C Ë D biçiminde gösterilir.
2. Özalt Küme
Bir kümenin, kendisinden farklı bütün alt kümelerine o kümenin özalt kümeleri denir.
3. Alt Kümenin Özelikleri
Her küme kendisinin alt kümesidir.
i) A Ì A
ii) Boş küme her kümenin alt kümesidir.
Æ Ì A
iii) (A Ì B ve B Ì A) Û A = B dir.
ıv) (A Ì B ve B Ì C) ise, A Ì C dir.
v) n elemanlı bir kümenin alt kümelerinin sayısı 2n ve özalt kümelerinin sayısı 2n – 1 dir.
| Ü | Elemanları arasında a bulunan n elemanlı bir kümenin,• alt kümelerinden 2n–1 tanesinde a bulunmaz.• alt kümelerinden 2n–1 tanesinde a bulunur. |
F. KÜMELERLE YAPILAN İŞLEMLER
A nın elemanlarından veya B nin elemanlarından oluşan kümeye bu iki kümenin birleşim kümesi denir ve A È B biçiminde gösterilir.1. Kümelerin Birleşimi
A È B = {x : x Î A veya x Î B} dir.
2. Birleşim İşleminin Özelikleri
a) A È Æ = A
b) A È A = A
c) A È B = B È A
d) A È (B È C) = (A È B) È C
e) A Ì B ise, A È B = B
f) A È B = Æ ise, (A = Æ ve B = Æ) dir.
3. Kümelerin Kesişimi
A ve B kümesinin ortak elemanlarından oluşan kümeye A ile B nin kesişim kümesi denir ve A Ç B biçiminde gösterilir.
d) (A Ç B) Ç C = A Ç (B Ç C)
e) A Ç (B È C) = (A Ç B) È (A Ç C)
f) A È (B Ç C) = (A È B) Ç (A È C)
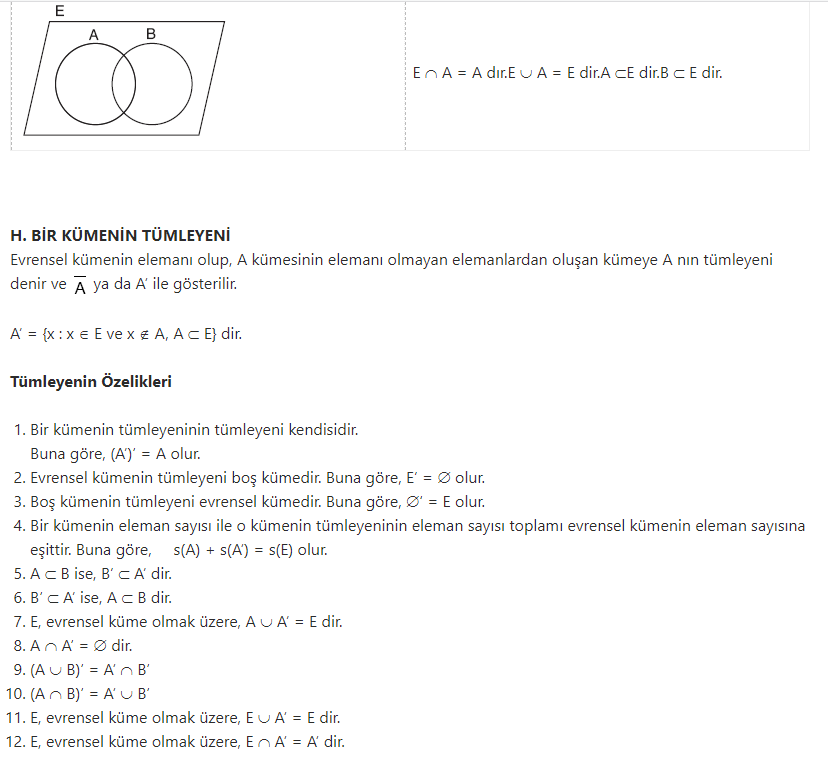
G. EVRENSEL KÜME
Üzerinde işlem yapılan, bütün kümeleri kapsayan kümeye, evrensel küme denir. Evrensel küme genellikle E ile gösterilir.I. KUVVET KÜMESİ
Bir kümenin bütün alt kümelerin kümesine kuvvet kümesi denir. Kuvvet kümesi P(A) ile gösterilir.
s(A) = n ise, s(P(A)) = 2n dir.
J. İKİ KÜMENİN FARKI
A kümesinde olup, B kümesinde olmayan elemanların kümesine A fark B kümesi denir. A fark B kümesi A – B ya da A B biçiminde gösterilir.
A – B = {x : x Î A ve x Ï B} dir.

Tenis veya voleybol oynayanların sayısı:
s(T È V) = a + b + c
Tenis ya da voleybol oynayanların sayısı:
s(T – V) + s(V – T) = a + c
Sadece tenis oynayanların sayısı:
s(T – V) = a


