- 24 Ara 2023
- 188
- 0
- 16
Bu ders notumuzda “Matematik: Birinci Dereceden Denklemler” başlığı altında; birinci dereceden denklemler, denklemlerin çözümü, ax + b = 0 denkleminin çözümü, ax + by + c = 0 birinci dereceden iki bilinmeyenli denklemin çözümü gibi konular hakkında detaylı bilgileri bulabilirsiniz.


C. ax + b = 0 DENKLEMİNİN ÇÖZÜM KÜMESİ

Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin BulunmasıBirinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.
a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
denklem sistemini göz önüne alalım:
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durum olduğu görülür.
Birinci durum:

Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir.
< → Küçüktür
> → Büyüktür
≤→ Küçük eşittir (Küçüktür veya eşittir)
≥→ Büyük eşittir (Büyüktür veya eşittir)

Eşitsizlikler sayı doğrusu üzerinde gösterilirken, eşitsizlik sembollerine dikkat etmek önemlidir. < ve > sembollerinde, sayılar çözüm kümesine dahil değilken, ≤ ve ≥ sembollerinde sayılar çözüm kümesine dahildir. Yani;
“x < 3” eşitsizliğine göre, bu eşitsizliği sağlayan sayılar 3’ten küçük olan tüm reel sayılardır ve 3 bu eşitsizliği sağlamaz.
“x ≤ 3” eşitsizliğine göre ise, bu eşitsizliği sağlayan sayılar 3 ve 3’ten küçük olan tüm reel sayılardır.
ÖRNEK: Aşağıda bazı eşitsizlikler ve bu eşitsizliklerin sayı doğrusu üzerinde gösterimleri verilmiştir. Dikkatle inceleyiniz.
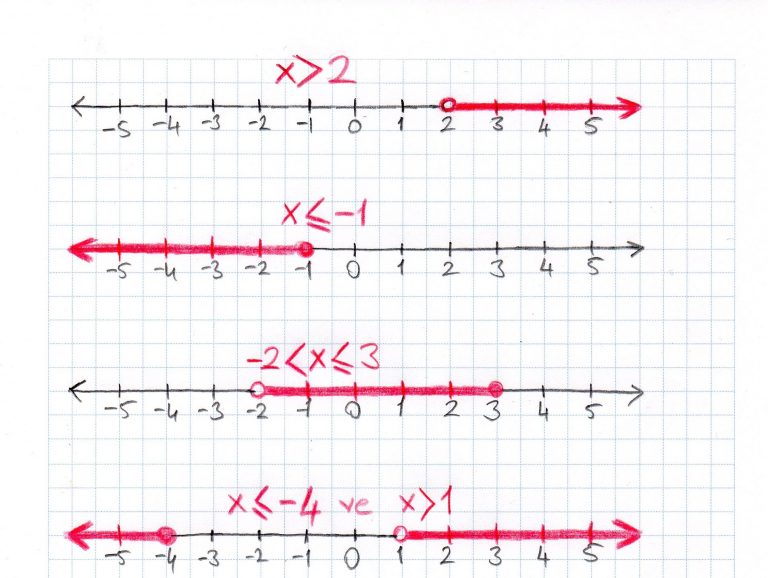
Yukarıdaki şemada eşitsizlikler ve bu eşitsizliklerin sayı doğrusu üzerindeki gösterimleri çizilmiştir. Eşitsizliklerin sayı doğrusu üzerindeki gösterimleri kırmızı renk ile belirtilmiştir. Kırmızı renkle çizilen alanlardaki tüm reel sayılar, ilgili eşitsizliği sağlayan sayılardır.
Eşitsizlikler sayı doğrusunda gösterilirken küçüktür (<) ve büyüktür (>) sembollerinde, sayının karşısına bir daire çizilir ve dairenin içi boş bırakılır. Küçük eşittir (≤) ve büyük eşittir (≥) sembollerinde ise sayıların karşısına çizilen dairelerin içleri doldurulur. Dolu daire, o sayının çözüm kümesinde yer aldığını gösterirken, boş daire o sayının çözüm kümesinde olmadığı anlamını taşır.
Eşitsizliklerin Çözümü
Değerli öğrenciler, eşitsizliklerin çözümü, denklem çözümüyle benzer bir mantık izler. Denklemi çözerken kullandığımız mantıkla eşitsizlikleri çözeriz. Hedefimiz, bilinmeyeni eşitsizliğin her iki tarafında da yalnız bırakmaktır. Bu amaçla, bilinmeyenin yanındaki sayılardan sırasıyla kurtulmaya çalışırız. Bu işlemi gerçekleştirirken öncelik sırasını tersten uygularız. Eşitsizlikleri çözerken aşağıdaki maddelere dikkat etmemiz önemlidir:

eşitsizliğini çözerken sırası ile aşağıdaki adımları izlememiz gerekir.
1) Önce eşitsizliğin her tarafından 8 çıkarırız.
5−8<−3y+8−8≤14−8−3<−3y≤6
bulunur.
2) Eşitsizliğin her tarafını -3’e bölmeliyiz. Yalnız negatif bir sayıya böldüğümüz için eşitsizliklerin yönünü değiştirmeyi unutmamalıyız.−3−3>−3y−3≥6−3
Bu işlemin sonucunda 1>y≥−2
bulunur. Bu eşitsizliği sayılar küçükten büyüğe doğru olacak şekilde düzenlersek;
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
A. TANIMa = b ise, a + c = b + c dir.
- Bir eşitliğin her iki tarafından aynı sayı çıkarılırsa eşitlik bozulmaz.
a = b ise, a – c = b – c dir.
- Bir eşitliğin her iki tarafı aynı sayı ile çarpılırsa eşitlik bozulmaz.
a = b ise, a × c = b × c dir.
C. ax + b = 0 DENKLEMİNİN ÇÖZÜM KÜMESİ
Birden fazla iki bilinmeyenli denklemden oluşan sisteme birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin BulunmasıBirinci dereceden iki bilinmeyenli denklem sistemlerinin çözüm kümesi; yok etme yöntemi, yerine koyma yöntemi, karşılaştırma yöntemi, grafik yöntemi, determinant yöntemi gibi yöntemlerden biri ile yapılır.
Biz burada üçünü vereceğiz.
a. Yok Etme Yöntemi: Değişkenlerden biri yok edilecek biçimde verilen denklem sistemi düzenlenir ve taraf tarafa toplanır.
| Taraf tarafa toplandığında veya çıkarıldığında (ya da bir düzenlemeden sonra) değişkenlerden biri sadeleşiyorsa “Yok etme yöntemi” kolaylık sağlar. |
b. Yerine Koyma Yöntemi: Verilen denklemlerin birinden, değişkenlerden biri çekilip diğer denklemde yerine yazılarak sonuca gidilir.
| Denklemlerin birinden, değişkenlerden biri kolayca çekilebiliyorsa, “Yerine koyma yöntemi” kolaylık sağlar. |
c. Karşılaştırma Yöntemi: Verilen denklemlerin ikisinden de aynı değişken çekilir. Denklemlerin diğer tarafları karşılaştırılır (eşitlenir).
| Her iki denklemden de aynı değişken kolayca çekilebiliyorsa, “Karşılaştırma yöntemi” kolaylık sağlar. |
| Ü | ax + by + c = 0dx + ey + f = 0 |
Bu iki denklemin her birinin düzlemde bir doğru belirttiği göz önüne alınırsa üç durum olduğu görülür.
denklem sisteminde,ise, bu iki doğru tek bir noktada kesişir.ax + by + c = 0
dx + ey + f = 0
Birinci durum:
Denklem sistemini sağlayan hiçbir nokta bulunamaz.
Bu durumda, verilen denklem sisteminin çözüm kümesi boş kümedir.
Eşitsizlikler
İçerisinde <,>,≤,≥ sembolleri bulunan ifadelere eşitsizlik denir. Eşitsizliklerin söylenişleri şu şekildedir:< → Küçüktür
> → Büyüktür
≤→ Küçük eşittir (Küçüktür veya eşittir)
≥→ Büyük eşittir (Büyüktür veya eşittir)
Eşitsizliklerin Sayı Doğrusunda Gösterimi
Eşitsizlikler sayı doğrusu üzerinde gösterilirken, eşitsizlik sembollerine dikkat etmek önemlidir. < ve > sembollerinde, sayılar çözüm kümesine dahil değilken, ≤ ve ≥ sembollerinde sayılar çözüm kümesine dahildir. Yani;
“x < 3” eşitsizliğine göre, bu eşitsizliği sağlayan sayılar 3’ten küçük olan tüm reel sayılardır ve 3 bu eşitsizliği sağlamaz.
“x ≤ 3” eşitsizliğine göre ise, bu eşitsizliği sağlayan sayılar 3 ve 3’ten küçük olan tüm reel sayılardır.
ÖRNEK: Aşağıda bazı eşitsizlikler ve bu eşitsizliklerin sayı doğrusu üzerinde gösterimleri verilmiştir. Dikkatle inceleyiniz.

Yukarıdaki şemada eşitsizlikler ve bu eşitsizliklerin sayı doğrusu üzerindeki gösterimleri çizilmiştir. Eşitsizliklerin sayı doğrusu üzerindeki gösterimleri kırmızı renk ile belirtilmiştir. Kırmızı renkle çizilen alanlardaki tüm reel sayılar, ilgili eşitsizliği sağlayan sayılardır.
Eşitsizlikler sayı doğrusunda gösterilirken küçüktür (<) ve büyüktür (>) sembollerinde, sayının karşısına bir daire çizilir ve dairenin içi boş bırakılır. Küçük eşittir (≤) ve büyük eşittir (≥) sembollerinde ise sayıların karşısına çizilen dairelerin içleri doldurulur. Dolu daire, o sayının çözüm kümesinde yer aldığını gösterirken, boş daire o sayının çözüm kümesinde olmadığı anlamını taşır.
Eşitsizliklerin Çözümü
Değerli öğrenciler, eşitsizliklerin çözümü, denklem çözümüyle benzer bir mantık izler. Denklemi çözerken kullandığımız mantıkla eşitsizlikleri çözeriz. Hedefimiz, bilinmeyeni eşitsizliğin her iki tarafında da yalnız bırakmaktır. Bu amaçla, bilinmeyenin yanındaki sayılardan sırasıyla kurtulmaya çalışırız. Bu işlemi gerçekleştirirken öncelik sırasını tersten uygularız. Eşitsizlikleri çözerken aşağıdaki maddelere dikkat etmemiz önemlidir:
- Eşitsizliklerin her iki tarafına aynı sayı eklenir veya her iki tarafından aynı sayı çıkarılırsa eşitsizlik yön değiştirmez.
- Bir eşitsizliğin her iki tarafı aynı pozitif sayı ile çarpılır veya aynı pozitif sayıya bölünürse eşitsizlik yön değiştirmez.
- Bir eşitsizliğin her iki tarafı aynı negatif sayı ile çarpılır veya aynı negatif sayıya bölünürse eşitsizlik yön değiştirir.
eşitsizliğini çözerken sırası ile aşağıdaki adımları izlememiz gerekir.
1) Önce eşitsizliğin her tarafından 8 çıkarırız.
5−8<−3y+8−8≤14−8−3<−3y≤6
bulunur.
2) Eşitsizliğin her tarafını -3’e bölmeliyiz. Yalnız negatif bir sayıya böldüğümüz için eşitsizliklerin yönünü değiştirmeyi unutmamalıyız.−3−3>−3y−3≥6−3
Bu işlemin sonucunda 1>y≥−2
bulunur. Bu eşitsizliği sayılar küçükten büyüğe doğru olacak şekilde düzenlersek;


